CONVEXITÉ - Fonctions convexes

CONVEXITÉ - Fonctions convexes

L’étude des fonctions convexes a permis de fournir un cadre dans lequel peut se résoudre toute une classe de problèmes d’analyse fonctionnelle non linéaire; les problèmes ainsi abordés sont des questions d’optimisation provenant de divers domaines: la mécanique, l’économie, les équations aux dérivées partielles, l’analyse numérique. Compte tenu de la difficulté d’aborder de manière un peu générale les problèmes non linéaires, c’est là un rôle très important qui a motivé le développement autonome de la théorie.

Les travaux de W. Fenchel, de T. Rockafellar, de J.-J. Moreau ont développé les outils de base de l’analyse convexe notamment la notion de fonctions convexes conjuguées et la notion de sous-différentiel qui sert de produit de remplacement pour les fonctions convexes non différentiables.

Nous renvoyons à l’article CONVEXITÉ - Ensembles convexes, pour tout ce qui concerne les résultats généraux sur les convexes et à l’article OPTIMISATION ET CONTRÔLE pour des exemples d’application de l’analyse convexe à l’optimisation.

1. Les fonctions convexes

Soit E un espace vectoriel sur R, C une partie convexe de E et f une fonction définie sur E à valeurs dans R 漣 (c’est-à-dire prenant éventuellement les valeurs 梁 秊). L’épigraphe de f , noté épi(f ), est l’ensemble des couples (x , a ) de C 憐 R tels que f (x ) 諒 a. La fonction f sera dite convexe si son épigraphe est une partie convexe de E 憐 R.

On obtient immédiatement une interprétation analytique de cette définition: La fonction f est convexe si et seulement si, pour tout réel de l’intervalle [0, 1], on a:

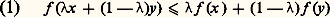pour tous les couples (x , y ) d’éléments de C ne vérifiant pas f (x ) = 漣 f (y ) = 梁 秊 (auquel cas le second membre de l’inégalité (1) n’est pas défini). En raisonnant par récurrence, on prouve que, si¹,², ...,ⁿ sont des réels positifs dont la somme est 1, on a:

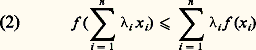chaque fois que le second membre de l’inégalité (2) a un sens.

La possibilité pour la fonction f de prendre la valeur + 秊 permet de ne considérer que des fonctions convexes définies sur E tout entier; en effet, si on prolonge la fonction f définie sur C en la fonction face="EU Caron" キ définie sur E en posant face="EU Caron" キ (x ) = + 秊 si x 殮 C, les fonctions f et face="EU Caron" キ ont alors le même épigraphe et donc f est convexe si et seulement si face="EU Caron" キ est convexe. Désormais, nous ne considérerons donc que des fonctions définies sur E tout entier. Cela nous conduit à définir le domaine effectif de f , noté dom (f ):

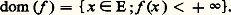Le domaine effectif de f est la projection sur E de l’épigraphe de f ; c’est une partie convexe de E.

La valeur 漣 秊 peut se présenter dans certains cas particuliers; nous ne l’éliminons pas a priori; néammoins, nous introduisons la terminologie suivante: La fonction convexe f est propre si son domaine effectif est non vide et si elle ne prend jamais la valeur 漣 秊; la restriction de f à dom (f ) est alors une fonction à valeurs dans R (cf. CONVEXITÉ - Ensembles convexes). Une fonction deux fois continûment différentiable sur un ouvert convexe C de Rⁿ à valeurs réelles est convexe si et seulement si la matrice hessienne:

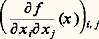est, en tout point x de C, la matrice d’une forme quadratique positive.

2. Cas de la dimension 1

L’exemple des fonctions convexes définies sur R est instructif pour l’étude ultérieure des fonctions convexes définies sur Rⁿ , ou même sur des espaces vectoriels topologiques. En outre, ce cas a un intérêt propre pour la définition d’une classe intéressante d’espaces: les espaces d’Orlicz. Dans tout ce chapitre 2, f est une fonction convexe propre définie sur R.

Supposons que x ¹, x ², x ³ soient dans dom (f ) et vérifient x ¹ 諒 x ² 諒 x ³; en remarquant que:

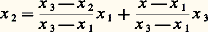et en appliquant l’inégalité (1), on obtient les inégalités:

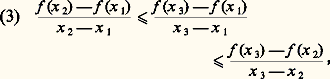c’est-à-dire que le coefficient directeur de la droite M¹M³ (cf. fig. 1) est compris entre celui de la droite M¹M² et celui de la droite M²M³. En se servant de ces inégalités, on montre que f est continue sur l’intérieur de son domaine effectif.

L’utilisation des inégalités (3) permet de montrer que, en tout point intérieur à dom f , la fonction f admet une dérivée à droite f ^d size=1(x ) et une dérivée à gauche f ^g size=1(x ) et qu’on a, en outre, f ^g size=1(x ) 諒 f ^d size=1(x ). De plus, f ^d (x ) est croissante et continue à droite sur l’intérieur de dom f. Si x ⁰ est un point intérieur à dom f tel que f (x ⁰) = 0, pour tout x intérieur à dom f , on peut écrire:

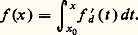Les N-fonctions

Considérons maintenant les fonctions convexes définies sur R à valeurs dans R et qui admettent une représentation de la forme:

où 﨏 est une fonction définie sur [0, + 秊[, croissante, continue à droite, nulle en 0, telle que: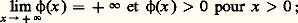

ces fonctions présentent un intérêt particulier pour la définition des espaces d’Orlicz; ce sont les N-fonctions. Il s’agit, en fait, des fonctions convexes paires définies sur R à valeurs dans R strictement croissantes sur [0, + 秊[, telles que:

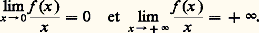Les N-fonctions vérifient, en outre, les inégalités (cf. fig. 2):

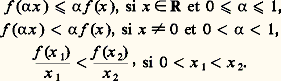Soit f une N-fonction exprimée sous la forme (4); posons:

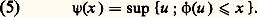Si 﨏 est continue strictement croissante, 祥 est la fonction réciproque de 﨏 (fig. 3).

Remarquons qu’à un intervalle sur lequel 﨏 est constante correspond un saut de la fonction 祥 et qu’à un saut de la fonction 﨏 correspond un intervalle sur lequel 祥 est constante; si l’on rajoute aux courbes représentatives de 﨏 et de 祥 les segments verticaux qui correspondent aux sauts des fonctions 﨏 et 祥 (ce sont les seules discontinuités possibles puisque ces fonctions sont monotones), on obtient des courbes symétriques par rapport à la première bissectrice. Une démarche analogue effectuée sur la fonction 祥 redonne la fonction 﨏.

Si, maintenant, on pose:

on obtient une N-fonction appelée fonction conjuguée de la fonction f.

L’inégalité suivante, appelée inégalité de Young, dont la signification géométrique obtenue en interprétant f (x ) et g (y ) comme des aires est suggérée sur la figure 4, a lieu:

L’égalité est atteinte lorsque x 閭 0 et y = 﨏 (x ); si bien que l’on a:

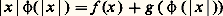et qu’on a de même:

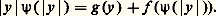Comme g (y ) 閭 xy 漣 f (x ) et que l’égalité a lieu pour au moins une valeur x ⁰ de x , on peut dire que:

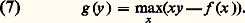Cette inégalité a une interprétation géométrique simple en introduisant le point M d’abscisse x sur la droite D passant par l’origine de coefficient directeur y et le point N d’abscisse x sur la courbe représentative de g (cf. fig. 5); alors:

Remarquons que, si f est dérivable, la tangente au graphe de f en ⁰ est parallèle à la droite D et l’équation de cette tangente est t (x ) = xy 漣 g (y ). La fonction g est la transformée de Legendre de f .

On peut aussi dire que la fonction t (x ) = xy 漣 g (y ) est la plus grande fonction affine de coefficient directeur y qui minore f .

Si p 礪 1, la fonction f (x ) = |x | p/p est un exemple de N-fonction; pour x 礪 0, on a f (x ) = x ^p-1 et (f )^-1(x ) = x ^q-1 , où 1/p + 1/q = 1; par conséquent la fonction g conjuguée de f est définie par g (x ) = |x | q/q .

Les espaces d’Orlicz

Soit f une N-fonction, notons l ^f l’ensemble des suites réelles (x ⁱ )ⁱ size=1^閭0 telles qu’il existe 見 礪 0 pour lequel: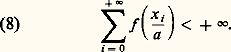

l ^f est un sous-espace vectoriel de l’espace des suites que l’on munit d’une norme en posant:

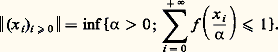Muni de cette norme, l ^f est un espace de Banach (cf. espaces vectoriels NORMÉS), appelé espace d’Orlicz de suites associé à la N-fonction f .

On peut montrer que l ^f est aussi l’ensemble des suites réelles (x ⁱ )ⁱ size=1^閭0 telles que:

où g est la fonction conjuguée de f .

On définit alors une autre norme sur l ^f en posant: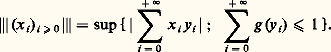

Cette norme est équivalente à la première; plus précisément:

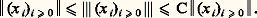Lorsque f vérifie, en outre, la condition:

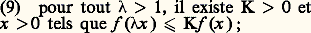ce qui se produit si et seulement si:

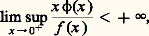l’espace l ^f est aussi l’espace des suites (x ⁱ )ⁱ size=1^閭0 tel que, pour tout 見 礪 0, l’inégalité (8) ait lieu; l ^f est alors un espace de Banach séparable; son dual est isomorphe à l ^g , où g est la conjuguée de f , grâce à l’isomorphisme:

où:

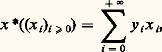avec:

L’application de ces considérations à la N-fonction f (x ) = |x | p/p , avec p 礪 1, donne pour espace d’Orlicz de suites l’espace l ^p (cf. espaces vectoriels NORMÉS). Une étude analogue peut être conduite dans le cadre de l’intégration, en définissant l’ensemble L^f (K) des fonctions x (t ), définies à un ensemble de mesure nulle près ^{[cf. INTÉGRATION ET MESURE]}, d’un compact K de Rⁿ , à valeurs dans R telles qu’il existe 見 礪 0 pour lequel on a:

Comme dans le cas des suites, L^f (K) est aussi l’ensemble des fonctions x (t ) pour lesquelles:

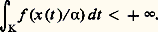
L^f (K) muni de l’une des deux normes équivalentes: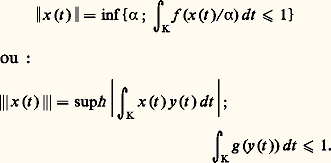

est un espace de Banach appelé espace d’Orlicz de fonctions associé à la N-fonction f .

3. Cas général

Dans ce chapitre, E désigne l’espace Rⁿ ou, plus généralement, un espace vectoriel topologique séparé localement convexe sur R; dans ce dernier cas, le dual topologique E de E sera muni de la topologie faible 精^s (E) donnée par E et E sera muni de la topologie faible 精^s (E) donnée par E.

Il ne faudrait pas croire que l’on peut, comme dans le cas des fonctions convexes de R dans R, conclure à la continuité des fonctions convexes de E dans R 漣; on dispose, en fait, du résultat suivant:

Soit f une fonction convexe prenant une valeur finie en un point x de E; s’il existe un voisinage de x sur lequel f est majorée par une constante finie, elle est continue au point x .

Ce résultat permet, dans le cas particulier où E = Rⁿ , d’établir que:

Toute fonction convexe propre sur Rⁿ est continue sur l’intérieur de son domaine effectif; en particulier, si f est à valeurs dans R, alors dom (f ) = Rⁿ et f est continue sur Rⁿ .

Rappelons qu’une fonction f de E dans R 漣 est dite semi-continue inférieurement si, pour tout réel a , l’ensemble des éléments x de E tels que f (x ) 諒 a est fermé; il est équivalent de dire que l’épigraphe de f est fermé, ou encore que f est enveloppe supérieure d’une famille de fonctions continues, c’est-à-dire que:

où f size=1^見 est continue pour tout 見 捻 a .

L’importance des hyperplans d’appui dans l’étude des ensembles convexes nous amène à introduire pour une fonction convexe f de E dans R 漣 la famille A^f des fonctions affines continues qui minorent f . Si on note 臨(E) l’ensemble des fonctions h de E dans R 漣 qui sont enveloppe supérieure d’une famille de fonctions affines continues, le théorème de séparation (cf. chap. 4 de l’article CONVEXITÉ – Ensembles convexes) permet de montrer que:

L’ensemble h est élément de 臨(E) si et seulement si h est une fonction convexe propre semi-continue inférieurement ou vaut identiquement 漣 秊.

Pour une fonction f de E dans R 漣, la plus grande fonction g de 臨(E) qui minore f est aussi l’enveloppe supérieure des fonctions affines continues qui minorent f ; dans le cas où f est une fonction convexe et où A^f est non vide, g est aussi la plus grande fonction semi-continue inférieurement qui minore f ; si bien que, lorsque f est de plus semi-continue inférieurement, f = g .

Fonction conjuguée d’une fonction convexe

L’inégalité d’Young du chapitre 2 s’écrit xy 漣 g (y ) 諒 f (x ), ce que l’on peut interpréter en disant que la fonction affine l (x ) = xy 漣 g (y ) est une minorante de f ; la fonction g (y ) est choisie de telle sorte que l (x ) soit la plus grande minorante affine de f de coefficient directeur y .

Si, maintenant, f est une fonction convexe de E dans R 漣, de la même façon, pour tout x 捻 E, introduisons la fonction affine l (x ) = x (x ) 漣 見 et cherchons à déterminer si possible 見, de manière à obtenir la plus grande minorante affine de f de forme linéaire associée x ; cela nous conduit à introduire:

Si f (x ) 捻 R, alors la fonction l (x ) = x (x ) 漣 f (x ) est effectivement la plus grande minorante affine continue de forme linéaire associée x .

La formule (10) généralise la transformation de Legendre (7) du chapitre 2 et permet de définir sur E une fonction f convexe qui est dans la classe 臨(E); la fonction f est, par définition, la fonction conjuguée de f .

Remarquons que si la fonction f (x ) est finie, de la formule (10) on tire l’inégalité de Young:

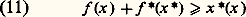qui généralise l’inégalité (6) du chapitre 2.

Recommençons maintenant le procédé en posant, pour tout x 捻 E,

f est alors le plus grand élément de 臨(E) qui minore f ; donc, si f 捻 臨(E), alors f = f .

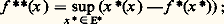Nous renvoyons au chapitre 1 de l’article OPTIMISATION ET CONTRÔLE pour voir comment intervient la fonction conjuguée dans certains problèmes d’optimisation.

Sous-différentiel

Soit f une fonction convexe de E dans R 漣. Supposons qu’il existe un élément l de A^f (c’est-à-dire une minorante affine continue de f ) tel que l (x ⁰) = f (x ⁰); on dit alors que f est sous-différentiable en x ⁰; l’application linéaire continue x associée à l’application affine l est un sous-gradient de f en x ⁰; l’ensemble des sous-gradients de f en x ⁰ est appelé le sous-différentiel en x ⁰ de f et est noté 煉f (x ⁰).

Remarquons que, dans ces conditions, on a:

l’hyperplan H graphe dans E 憐 R de l est un hyperplan d’appui du convexe épi(f ) (fig. 6). Comme on a vu, par ailleurs, que la plus grande minorante affine continue de f ayant x pour application linéaire associée est donnée par x (z ) 漣 f (x ), on en conclut que f (x ) = x (x ⁰) 漣 f (x ⁰); en fait, cette égalité est une conditon nécessaire et suffisante pour que x 捻 煉f (x ⁰).

Si f est dans 臨(E) (cas où f = f ), les propositions suivantes sont équivalentes:

Le sous-différentiel en x ⁰ d’une fonction convexe f est un sous-ensemble convexe fermé de E.

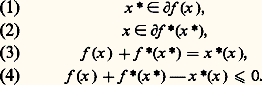Le résultat suivant donne une condition intéressante de sous-différentiabilité d’une fonction convexe:

Si f est finie et continue en un point x ⁰, f est sous-différentiable en tout point intérieur de dom(f ) et en particulier en x ⁰.

Dans le cas où f est Gâteaux-différentiable en x ⁰, c’est-à-dire s’il existe un élément f (x ⁰) de E tel que, pour tout y de E, on ait:

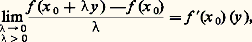la fonction f est sous-différentiable en x ⁰ et f (x ⁰) est l’unique sous-gradient de f en x ⁰. Réciproquement si, en x ⁰, f est continue, sous-différentiable et ne possède qu’un seul sous-gradient x , alors f est Gâteaux-différentiable en x ⁰ et f (x ⁰) = x .

Le sous-différentiel permet de remplacer la différentielle et d’exprimer notamment des conditions d’optimalité dans des problèmes de contrôle (cf. OPTIMISATION ET CONTRÔLE, chap. 2).

Donnons l’exemple de la fonction F, définie sur L²( 行), où 行 est un ouvert de Rⁿ suffisamment régulier, par:

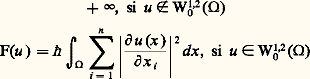W^01,2( 行) représente ici le sous-espace de l’espace de Sobolev W¹,²( 行) (cf. espaces vectoriels NORMÉS) constitué des u dont la restriction au bord de a est nulle.

F est alors une fonction convexe semi-continue inférieurement, sous-différentiable en chaque point de W^01,2( 行) 惡 W²,²( 行); pour chaque point u de ce sous-espace, le sous-différentiel 煉F(u ) est constitué du seul élément:

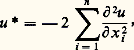c’est-à-dire que, pour v 捻 L²( 行), on a:

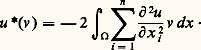Notons encore que, si f est une fonction convexe propre de 臨(E) pour tous les x ¹, x ², x ¹, x ² vérifiant x ¹ 捻 煉 f (x ¹) et x ² 捻 煉f (x ²), on a:

On dit que le sous-différentiel est un opérateur monotone; il est même maximal monotone en ce sens que, pour tout couple (x , x ) tel que x 捻 煉f (x ), il existe un couple (y , y ) tel que: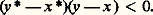

La théorie des opérateurs maximaux monotones, qui généralise l’analyse convexe, est très utile pour l’étude des équations d’évolution non linéaires de type parabolique ou hyperbolique.

Encyclopédie Universelle. 2012.